piPrimeShapesForLenghtNseq.nb

${U == 1 + z, S == U + S T U z^2, T == z^3 + 2 T z^3 + T z^4 + S T^2 U^2 z^4, S0 == S + S0 z}$

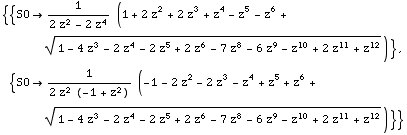
One of these 2 is the generating function. Setting z=0, we can quickly see that first one blows up as z->0 so must be second one.

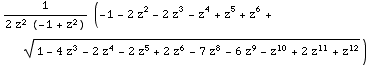
1/(2 z^2 (-1 + z^2)) (-1 - 2 z^2 - 2 z^3 - z^4 + z^5 + z^6 + (1 - 4 z^3 - 2 z^4 - 2 z^5 + 2 z^6 - 7 z^8 - 6 z^9 - z^10 + 2 z^11 + z^12)^(1/2))

Singularity occurs either where denominator is zero (0 or ±1, but we know analytic at z=0 as it is a generating function.) or where square root is zero. Let's find where square root is zero.

This is our (unique) dominant singularity. (It is smaller in magnitude than the singularities z=±1 caused by the denominator.)

The next few commands are to simply divide poly by (1-z/r) to get poly2 and then check that this worked.

1 + 1.80776 z + 3.26799 z^2 + 1.90775 z^3 + 1.44875 z^4 + 0.618994 z^5 + 3.11899 z^6 + 5.63839 z^7 + 3.19285 z^8 - 0.228094 z^9 - 1.41234 z^10 - 0.553171 z^11 + 4.54747*10^-13 z^14 + O[z]^15

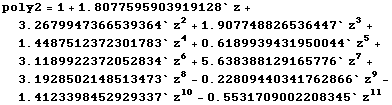
poly2 = 1 + 1.80776 z + 3.26799 z^2 + 1.90775 z^3 + 1.44875 z^4 + 0.618994 z^5 + 3.11899 z^6 + 5.63839 z^7 + 3.19285 z^8 - 0.228094 z^9 - 1.41234 z^10 - 0.553171 z^11

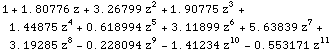
1 + 1.80776 z + 3.26799 z^2 + 1.90775 z^3 + 1.44875 z^4 + 0.618994 z^5 + 3.11899 z^6 + 5.63839 z^7 + 3.19285 z^8 - 0.228094 z^9 - 1.41234 z^10 - 0.553171 z^11

This is close to poly, so our polynomial division worked.

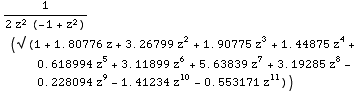
1/(2 z^2 (-1 + z^2)) (√ (1 + 1.80776 z + 3.26799 z^2 + 1.90775 z^3 + 1.44875 z^4 + 0.618994 z^5 + 3.11899 z^6 + 5.63839 z^7 + 3.19285 z^8 - 0.228094 z^9 - 1.41234 z^10 - 0.553171 z^11))