eqn = {S == z * S + A, A == z^2 * A * B + z^2 * B, B == z^2 * A * B + z^3}

{S == A + S z, A == B z^2 + A B z^2, B == A B z^2 + z^3}

solset = Simplify[Solve[eqn, S, {A, B}]]

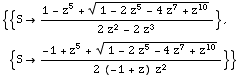
{{S→ (1 - z^5 + (1 - 2 z^5 - 4 z^7 + z^10)^(1/2))/(2 z^2 - 2 z^3)}, {S→ (-1 + z^5 + (1 - 2 z^5 - 4 z^7 + z^10)^(1/2))/(2 (-1 + z) z^2)}}

Here are the 2 possibilities for the generating function.  We choose the one that does not blow up at 0.

sol = S/.Part[solset, 2, 1]

(-1 + z^5 + (1 - 2 z^5 - 4 z^7 + z^10)^(1/2))/(2 (-1 + z) z^2)

The dominant singularity will occur where the square root evaluates to 0, or
where the denominator is 0 (z = 1,  but not z = 0, actually analytic there),
whichever is closest to origin.

poly = 1 - 2 z^5 - 4 z^7 + z^10

1 - 2 z^5 - 4 z^7 + z^10

solset = NSolve[poly == 0, z]

r = z/.Part[solset, 9, 1]

0.756328

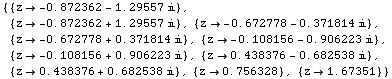
This gives us our dominant singularity, r.

1/r

1.32218

This is our exponential growth rate.

p2a = poly/(1 - z/r)

(1 - 2 z^5 - 4 z^7 + z^10)/(1 - 1.32218 z)

Series[p2a, {z, 0, 10}]

1 + 1.32218 z + 1.74816 z^2 + 2.31137 z^3 + 3.05605 z^4 + 2.04064 z^5 + 2.69809 z^6 - 0.432643 z^7 - 0.572031 z^8 - 0.756328 z^9 - 3.55271*10^-15 z^10 + O[z]^11

This is how we have figured to divide polynomials in Mathematica.  Since r is only a numerical approximation, p2a is not actually a polynomial gotten by dividing out one root, but it is really close to one.  By cutting and pasting the above, we can get a polynomial p2 such that p2*(1-z/r) is very close to poly.  That is all we need.

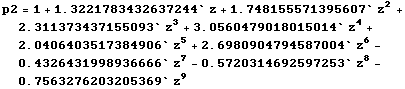
p2 = 1 + 1.32218 z + 1.74816 z^2 + 2.31137 z^3 + 3.05605 z^4 + 2.04064 z^5 + 2.69809 z^6 - 0.432643 z^7 - 0.572031 z^8 - 0.756328 z^9

1 + 1.32218 z + 1.74816 z^2 + 2.31137 z^3 + 3.05605 z^4 + 2.04064 z^5 + 2.69809 z^6 - 0.432643 z^7 - 0.572031 z^8 - 0.756328 z^9

Expand[p2 * (1 - z/r)]

1 + 0. z + 0. z^2 + 0. z^3 + 0. z^4 - 2. z^5 - 8.88178*10^-16 z^6 - 4. z^7 - 7.77156*10^-16 z^8 + 7.77156*10^-16 z^9 + 1. z^10

(Very close to p1, so p2 is what we want.)

sol

(-1 + z^5 + (1 - 2 z^5 - 4 z^7 + z^10)^(1/2))/(2 (-1 + z) z^2)

left = Sqrt[p2]/(2 (-1 + z) * z^2)

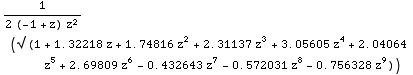
1/(2 (-1 + z) z^2) (√ (1 + 1.32218 z + 1.74816 z^2 + 2.31137 z^3 + 3.05605 z^4 + 2.04064 z^5 + 2.69809 z^6 - 0.432643 z^7 - 0.572031 z^8 - 0.756328 z^9))

Remember, only the part that was next to the dominant singularity will matter.

K = 1/Gamma[-1/2] * left/.z→r

2.44251

1/r

1.32218

Remember alpha=1/2 as the singularity was (1-z/r)^(1/2), and that exponent gives us alpha.  We then know we have a factor of n^(-alpha-1)

So S_n ~ 2.44251*1.32218^n * n^(-3/2)

Created by Mathematica  (December 22, 2006) Valid XHTML 1.1!