Proof of bijection between Pi-Shapes of size 2n+2 and Motzkin of size n

Starting from the grammar for the pi-shapes:

  S -> [T]S | epsilon
  T -> [T][T]S | epsilon

The system translate into a system of equations on the generating functions, thanks to the DSV method:

>	Sys1:={S=z^2*S*T+1,T=z^4*S*T^2+1};

>	Sol1:=allvalues(solve(Sys1,{S,T}));

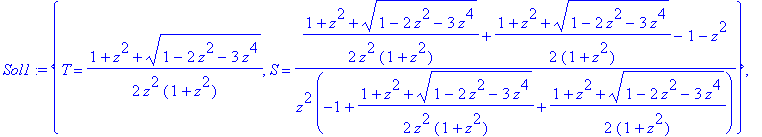
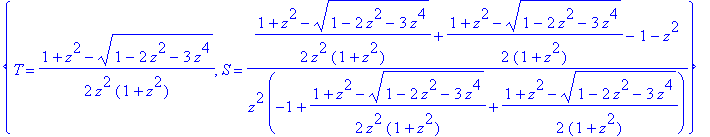
Now we choose the solution for S(z) having positive coefficients, thus:

>	Res1 := simplify(rhs(Sol1[2][2]));

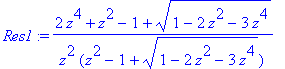
>	series(simplify(Res1),z,35);

Starting from the grammar for the pi-shapes:

  M -> [M]M | .M | epsilon
The system translate into a system of equations, that we solve:

>	Sys2:={M=z^2*M^2+z*M+1};

>	Sol2:=solve(Sys2,{M});

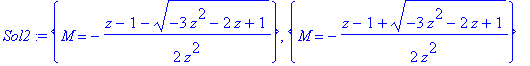
Once again, we pick the solution whose coefficients are positive in a taylor expansion around z=0

>	Res2 := rhs(Sol2[2][1]);

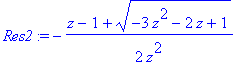
>	series(simplify(Res2),z,35);

The resulting generating functions, although having very different expressions, turn out to be equivalent upon substitution of z with z^2 in that of Motzkin followed by a z^2 multiplication.

>	simplify(Res1-1-z^2*subs(z=z^2,Res2));

Thus the n-th coefficients of the generating function for the Motzkin words is equal to the 2n+2-th coefficient of that of the pi-shapes