
A B C D --------------------------------- A| 0 1 2 1 B| 1 0 1 1 C| 2 1 0 3 D| 1 1 3 0Let's agree that the taxa (species,leaves) are called A,B,C,D and that we will represent the distance between any two clusters at any time by a distance array, called dist, which is initialized as previously. In the first step of UPGMA, we have a "tree" consisting of 4 singleton clusters, with no connections.

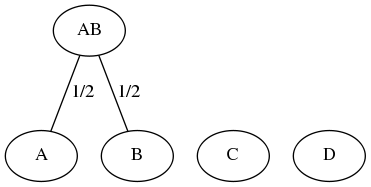
We next determine the minimum distance dmin in the array; i.e. dmin = 1 and determine the first row and column, in a top-down, left-right manner, for which dist(row,col)=dmin. Since dist({A},{B})=1=dmin, we combine the elements of cluster {A} and cluster {B} to form the agglomerated cluster {A,B}, which is defined to be the parent of both. The distance from the parent {A,B} to the leaves of each child (which in this case comprises A and B, but in general will be an intermediate node of the tree) is defined to be dmin/2 = 0.5. We then update the distance between the new parent cluster {A,B} and all remaining clusters that are distinct from the two clusters that were combined to form the parent using the formula d({A,B},x) = (1 · d1 + 1 · d2)/(1+1) since the size of cluster {A} [resp. {B}] is 1. This leads to the following, which is identical to the previous case of WPGMA:
A,B C D
---------------------------------
A,B| 0 (2+1)/2 (1+1)/2
C | 1.5 0 3
D | 1 3 0
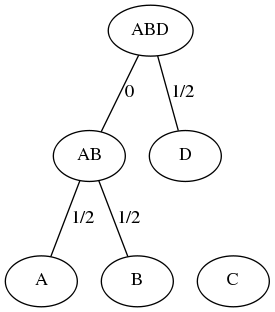
We next determine the minimum distance dmin in the array; i.e. dmin = 1 and determine the first row and column, for which dist(row,col)=dmin. Since dist({A,B},{D})=1=dmin, we combine the elements of cluster {A,B} and cluster {D} to form the agglomerated cluster {A,B,D}. The new cluster {A,B,D} is defined to be the parent of the child clusters {A,B} and {D}, and the distance from the parent to the leaves of each child cluster is defined to be dmin/2=0.5. Notice that this means that the distance from {A,B,D} to {A,B} must be zero, since the distance from {A,B} to each of {A} and {B} is 0.5. The UPGMA distance from {A,B,D} to {C} is defined to be (2 · 1.5 + 1 · 3)/(2+1) = 6/3 = 2, which is different from the value of (1.5+3)/2 = 9/4 = 2.25 obtained by WPGMA. NOTE also that an equivalent manner of updating the UPGMA distance d(C1,C2) between cluster C1 and cluster C2 is to find the average distance from all leaves of cluster C1 to all leaves of cluster C2. This involves |C1| · |C2| many multiplications, so for anything except a toy problem, it is useful to use the UPGMA formula. We then update the distance matrix:
A,B,D C
---------------------------------
A,B,D| 0 (2 · 1.5 + 1 · 3)/(2+1) = 6/3=2
C | 2 0
The minimum distance dmin in the array is 2; i.e. dist({A,B,D},{C})=2=dmin. We combine the elements of cluster {A,B,D} and cluster {C} to form the agglomerated cluster {A,B,C,D}. The new cluster {A,B,C,D} is defined to be the parent of the child clusters {A,B,D} and {C}, and the distance from the parent to the leaves of the child clusters is defined to be dmin/2=1. It follows that the distance from {A,B,C,D} to {A,B,D} must be 1 - 1/2 = 1/2. As well, the distance from {A,B,C,D} to {C} must be 1.

Finally, notice that UPGMA always produces an ultrametric tree, i.e. with the property that the distance from root to each leaf is the same.
NOTE that the final distances between taxa in the ultrametric tree do NOT agree with the distances from the initial distance matrix, since distance between C,D is 2 in the tree, but 3 in the distance matrix. This is because the intial distances do not satisfy the 3-point property, which states that for all points x,y,z we have D(x,z) ≤ max{D(x,y),D(y,z)}. Compare this with the triangle inequality (required for any metric) which states that for 3 points x,y,z two distances are equal and greater than or equal to the third: D(x,z) ≤ D(x,y)=D(y,z). Compare this with the triangle inequality that requires that D(x,z) ≤ D(x,y)+D(y,z).
Note that the given distance matrix does not satisfy the 3-point property, since for points A,B,C we have D(A,C) ≥ D(A,B)=D(B,C).
The output of my program (if you can compile it on your computer and run it on the folowing distance matrix
0.00 1.00 2.00 1.00 1.00 0.00 1.00 1.00 2.00 1.00 0.00 3.00 1.00 1.00 3.00 0.00then we obtain
0.00 1.00 2.00 1.00 1.00 0.00 1.00 1.00 2.00 1.00 0.00 3.00 1.00 1.00 3.00 0.00 0.00 0.00 1.50 1.00 0.00 0.00 0.00 0.00 1.50 0.00 0.00 3.00 1.00 0.00 3.00 0.00 0.00 0.00 2.25 0.00 0.00 0.00 0.00 0.00 2.25 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 --------2 | --------1.12 | --------3 | --------0.50 | --------1 | --------0.50 | --------0Hopefully you see how to interpret the output of the program in light of the discussion above.