
A B C D --------------------------------- A| 0 1 2 1 B| 1 0 1 1 C| 2 1 0 3 D| 1 1 3 0Let's agree that the taxa (species,leaves) are called A,B,C,D and that we will represent the distance between any two clusters at any time by a distance array, called dist, which is initialized as previously. In the first step of WPGMA, we have a "tree" consisting of 4 singleton clusters, with no connections.

We next determine the minimum distance dmin in the array; i.e. dmin = 1 and determine the first row and column, in a top-down, left-right manner, for which dist(row,col)=dmin. Since dist({A},{B})=1=dmin, we combine the elements of cluster {A} and cluster {B} to form the agglomerated cluster {A,B}, which is defined to be the parent of both. The distance from the parent {A,B} to the leaves of each child cluster (and not to the child cluster itself) is defined to be dmin/2 = 0.5. We then update the distance between the new parent cluster {A,B} and all remaining clusters that are distinct from the two clusters that were combined to form the parent. This leads to:
A,B C D
---------------------------------
A,B| 0 (2+1)/2 (1+1)/2
C | 1.5 0 3
D | 1 3 0

We next determine the minimum distance dmin in the array; i.e. dmin = 1 and determine the first row and column, for which dist(row,col)=dmin. Since dist({A,B},{D})=1=dmin, we combine the elements of cluster {A,B} and cluster {D} to form the agglomerated cluster {A,B,D}. The new cluster {A,B,D} is defined to be the parent of the child clusters {A,B} and {D}, and the distance from the parent to the leaves of the child clusters is defined to be dmin/2=0.5. Notice that this means that the distance from {A,B,D} to {A,B} must be zero, since the distance from {A,B} to each of {A} and {B} is 0.5. As well, the distance from {A,B,D} to {D} is 0.5. We update the distance matrix:
A,B,D C
---------------------------------
A,B,D| 0 (1.5+3)/2
C | 9/4 0

The minimum distance dmin in the array is 9/4; i.e. dist({A,B,D},{C})=2.25=dmin. We combine the elements of cluster {A,B,D} and cluster {C} to form the agglomerated cluster {A,B,C,D}. The new cluster {A,B,C,D} is defined to be the parent of the child clusters {A,B,D} and {C}, and the distance from the parent to the leaves of the child clusters is defined to be dmin/2=9/8=1.125. It follows that the distance from {A,B,C,D} to {A,B,D} must be 9/8 - 1/2 = 5/8 = 1.125-0.5 =0.625. As well, the distance from {A,B,C,D} to {C} must be 9/8=1.125.
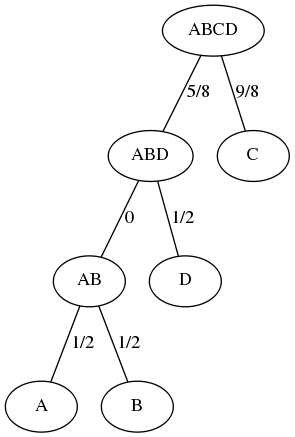
Finally, notice that WPGMA always produces an ultrametric tree, i.e. with the property that the distance from root to each leaf is the same.
NOTE that the final distances between taxa in the ultrametric tree do NOT agree with the distances from the initial distance matrix. This is because the intial distances do not satisfy the 3-point property, which states that for all points x,y,z we have D(x,z) ≤ max{D(x,y),D(y,z)}. Compare this with the triangle inequality (required for any metric) which states that for 3 points x,y,z two distances are equal and greater than or equal to the third: D(x,z) ≤ D(x,y)=D(y,z). Compare this with the triangle inequality that requires that D(x,z) ≤ D(x,y)+D(y,z).
Note that the given distance matrix does not satisfy the 3-point property, since for points A,B,C we have D(A,C) ≥ D(A,B)=D(B,C).
The output of my program (if you can compile it on your computer and run it on the distance matrix Kaitlin suggested), then we obtain
0 0 1.5 1 0 0 0 0 1.5 0 0 3 1 0 3 0 0 0 2.25 0 0 0 0 0 2.25 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 --------2 | --------1.125 | --------3 | --------0.5 | --------1 | --------0.5 | --------0Hopefully you see how to interpret the output of the program in light of the discussion above.